There is an old solitaire I started to play when I was in high school, when classes became too boring. I don’t know if it has a name or if I invited it ex nihilo. These are the rules:
- It begins with an empty 10x10 matrix
- Write a 1 where ever you want
- To write the next number you have to leave two blank squares if you move horizontally or vertically, if you move in diagonal you have to leave one blank square.
- Can you reach 100?
I played it a lot while in high school and college but never reached 100, mid 90s was my best move. My maths has never been good enough to let me prove if the game has solution and how many.
Some weeks ago I attended a boring conference and I discovered my self playing this old game again. But this time was different, this time I thaughth “R can show me the way to win”.
My first move was to use brute force, code a script that plays the game and play it hundreds of thousands of times. I did it.
set.seed(seed = 1000)
tabla_vacia <- function(ns=10){
tv <- matrix(data = 0,nrow = ns,ncol = ns)
return(tv)
}
posicion_inical <- function(ns=10,fijo=FALSE){
if(!fijo){
inicio <- sample(x = 1:ns,size = 2,replace = TRUE)
} else {
inicio <- fijo
}
return(inicio)
}
elige_movimiento <- function(movimientos_posibles){
move <- sample(x = movimientos_posibles,size = 1)
return(move)
}
traduce_movimiento <- function(move){
#1 arriba
#2 derecha
#3 abajo
#4 izquierda
#5 arriba derecha
#6 abajo derecha
#7 abajo izquierda
#8 arriba izquierda
if (move==1) {desp <- c(0,-3)}
if (move==2) {desp <- c(3,0)}
if (move==3) {desp <- c(0,3)}
if (move==4) {desp <- c(-3,0)}
if (move==5) {desp <- c(2,-2)}
if (move==6) {desp <- c(2,2)}
if (move==7) {desp <- c(-2,2)}
if (move==8) {desp <- c(-2,-2)}
return(desp)
}
comprueba_movimiento <- function(tabla,posicion,desp,ns=10){
posicion_nueva <- posicion + desp
if(posicion_nueva[1] %in% 1:ns & posicion_nueva[2] %in% 1:ns){
if(tabla[posicion_nueva[1],posicion_nueva[2]]==0){
comprueba <- 1
} else {
comprueba <- 0
}
} else {
comprueba <- 0
}
return(comprueba)
}
juega <- function(ns=10,fijo=FALSE){
tabla <- tabla_vacia(ns = ns)
posicion <- posicion_inical(ns = ns,fijo = fijo)
todos_movimientos <- 1:8
for (n in 1:100){
tabla[posicion[1],posicion[2]] <- n
movimientos_posibles <- todos_movimientos
move <- elige_movimiento(movimientos_posibles)
desp <- traduce_movimiento(move = move)
comprueba <- 0
while(comprueba!=1){
comprueba <- comprueba_movimiento(tabla=tabla,posicion = posicion,desp = desp,ns = ns)
if(comprueba==1){
posicion <- posicion + desp
n <- n+1
tabla[posicion[1],posicion[2]] <- n
} else {
movimientos_posibles <- movimientos_posibles[movimientos_posibles!=move]
if(length(movimientos_posibles)==0){
return(list(tabla=tabla,n=n))
}
move <- elige_movimiento(movimientos_posibles = movimientos_posibles)
desp <- traduce_movimiento(move = move)
}
}
}
return(list(tabla=tabla,n=n))
}
juega_a_saco <- function(N=10000,ns=10,fijo=FALSE){
mejor <- juega(ns=ns,fijo = fijo)
resul <- vector("numeric",N)
for (i in 1:N){
nueva <- juega(ns=ns,fijo = fijo)
resul[i] <- nueva$n
if (nueva$n>mejor$n){
mejor <- nueva
print(mejor$n)
}
}
print(mejor)
return(resul)
}This execution plays 10000 solitaires
resul <- juega_a_saco(N = 10000)## [1] 75
## [1] 83
## [1] 86
## [1] 88
## [1] 91
## $tabla
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 66 18 53 65 17 54 30 42 55 29
## [2,] 85 0 0 84 60 0 33 59 0 40
## [3,] 20 0 16 19 52 43 56 51 31 57
## [4,] 67 1 86 64 4 83 61 41 34 28
## [5,] 15 0 21 14 88 22 32 58 90 39
## [6,] 79 63 68 78 62 44 5 50 47 0
## [7,] 70 2 87 23 3 82 89 38 35 27
## [8,] 12 77 72 13 6 75 48 9 91 49
## [9,] 80 24 69 81 25 45 36 26 46 37
## [10,] 71 0 11 76 73 10 7 74 0 8
##
## $n
## [1] 91hist(resul)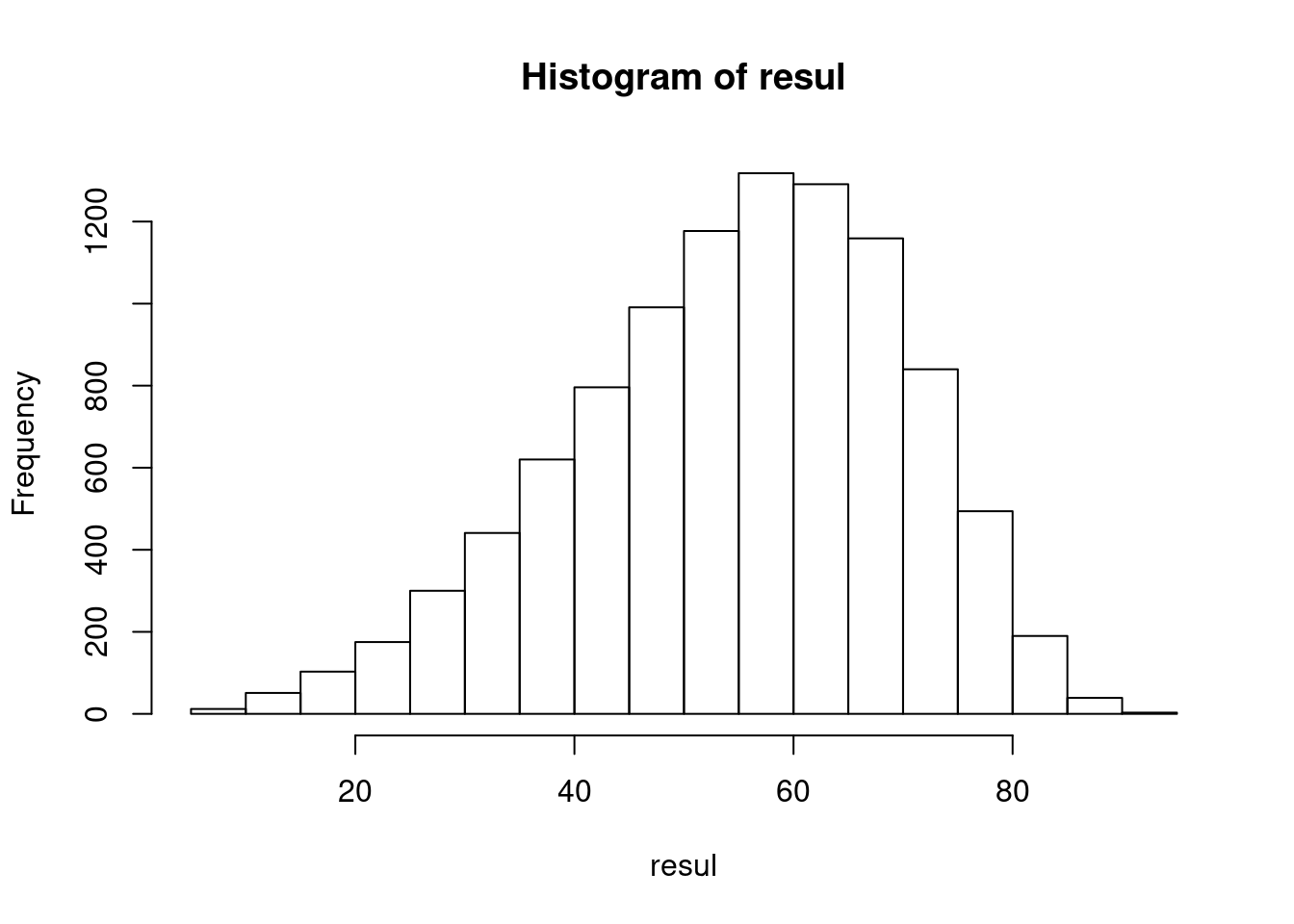
I tried harder with 100000000 solitaires and I get 99. But, where is the perfect game?
So my next move was clear, leave brute force strategy and embrace a new one: decompose the problem. This line play 1000 solitaires of 5x5 squares
resul2 <- juega_a_saco(N = 1000,ns = 5)## [1] 25
## $tabla
## [,1] [,2] [,3] [,4] [,5]
## [1,] 24 11 6 25 12
## [2,] 8 21 14 9 20
## [3,] 16 4 1 17 5
## [4,] 23 10 7 22 13
## [5,] 2 18 15 3 19
##
## $n
## [1] 25hist(resul2)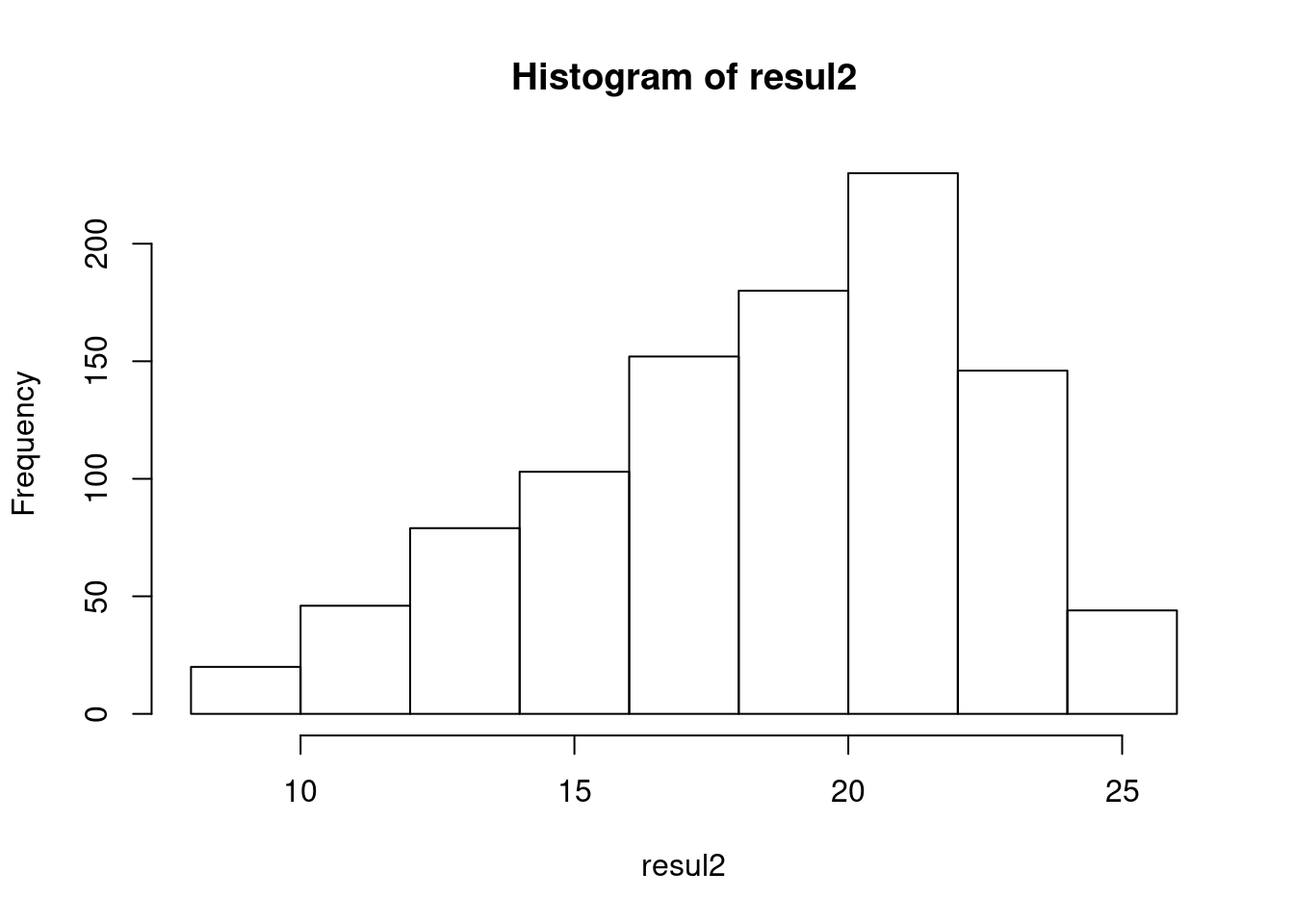
It’s very easy to find a solution for a 5x5 game, so the next move is to link this solutions.
banco_de_cuadros_correctos <- function(N=10000,ns=10,fijo=FALSE){
resul <- vector("list",N)
for (i in 1:N){
resul[[i]] <- juega(ns = ns,fijo = fijo)
}
resul <- resul[lapply(resul, function(x) x$n)==25]
return(resul)
}
todos_los_cuadros_correctos <- function(ns=10,N=1000){
muestras <- vector("list",ns*ns)
k <- 1
for (i in 1:ns){
for (j in 1:ns){
muestras[[k]]$inicio <- c(i,j)
muestras[[k]]$tablas <- banco_de_cuadros_correctos(N = N,ns = ns,fijo = c(i,j))
k <- k + 1
}
}
return(muestras)
}With this line you have a workbench with a bunch of solutions for every initial position in a 5x5 game.
tablas <- suppressWarnings(todos_los_cuadros_correctos(ns = 5,N = 1000))Let’s start from 1,1
tablas[[1]]$tablas[[1]]$tabla## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 12 17 2 9
## [2,] 6 22 25 5 19
## [3,] 14 3 8 13 16
## [4,] 24 11 18 23 10
## [5,] 7 21 15 4 20It finishes in 2,3 so let’s move to the right and so we have to link with a solitaire startign in 2,1
tablas[[6]]$tablas[[1]]$tabla## [,1] [,2] [,3] [,4] [,5]
## [1,] 24 12 18 23 11
## [2,] 1 21 9 14 20
## [3,] 7 16 3 6 17
## [4,] 25 13 19 22 10
## [5,] 2 5 8 15 4This one finishes in 4,1, now move in diagonal downwards and to the right and link with a table starting in 1,3
tablas[[3]]$tablas[[1]]$tabla## [,1] [,2] [,3] [,4] [,5]
## [1,] 7 19 1 6 18
## [2,] 12 22 25 15 10
## [3,] 2 5 8 20 4
## [4,] 24 16 11 23 17
## [5,] 13 21 3 14 9This one finishes in 2,3, now move to the left and let’s link with a new one starting in 2,5
tablas[[10]]$tablas[[1]]$tabla## [,1] [,2] [,3] [,4] [,5]
## [1,] 21 15 7 20 14
## [2,] 5 18 23 11 1
## [3,] 25 9 3 16 8
## [4,] 22 12 6 19 13
## [5,] 4 17 24 10 2Now, i’m going to put the all together from 1 to 100
t1 <- tablas[[1]]$tablas[[1]]$tabla
t2 <- tablas[[6]]$tablas[[1]]$tabla + 25
t3 <- tablas[[3]]$tablas[[1]]$tabla + 50
t4 <- tablas[[10]]$tablas[[1]]$tabla + 75
tA <- cbind(t1,t2)
tB <- cbind(t4,t3)
t <- rbind(tA,tB)
t## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 1 12 17 2 9 49 37 43 48 36
## [2,] 6 22 25 5 19 26 46 34 39 45
## [3,] 14 3 8 13 16 32 41 28 31 42
## [4,] 24 11 18 23 10 50 38 44 47 35
## [5,] 7 21 15 4 20 27 30 33 40 29
## [6,] 96 90 82 95 89 57 69 51 56 68
## [7,] 80 93 98 86 76 62 72 75 65 60
## [8,] 100 84 78 91 83 52 55 58 70 54
## [9,] 97 87 81 94 88 74 66 61 73 67
## [10,] 79 92 99 85 77 63 71 53 64 59Is this any useful? No, it’s totally useless. What can I learn from this? Brute force it’s a bad approach when your problem has infinite possibilities and you don’t know if it has one solution, many solutions, infinite solutions or not solutions at all. But decomposing the problem in more manageable parts it’s allways a good practice.
Has anyone better maths than me and can give me any mathematical hint about this solitaire?